|
مقاله دانشجویی تحقیق پروزه ومفالات دانشجویی
|
||
|
|
عَدَد یا یکی از مفاهیم پایه ریاضیات است. در آغاز عدد برای شمارش و اندازهگیری بهکار میرفت ولی بعدها ریاضیدانان مفهوم آن را توسعه دادند و مفهوم عدد صفر و عدد منفی و عدد موهومی و عدد مختلط را ابداع کردند.
عدد را نباید با رقم اشتباه کرد. رقم نشانهای است که برای نوشتن عدد بهکار میرود. تاریخ پیدایش عدد در آغاز، عدد به صورت محدود خود بود. حتی عدد را تا ۲ بیشتر نمیتوانستند بشمارند. برای عدد، مرزی برای شمار داشتند. برای نمونه،زمانی در بسیاری جاها، مرز شمار، عدد ۶ بود. تا ۶ میشمردند و پس از آن را میگفتند «بسیار». هنوز هم در بسیاری زبانها «هفت» به معنای بسیار است. در زبان فارسی، ضرب المثلی است که میگوید: «هفت بار گز کن، یکبار پاره کن.» در این ضرب المثل، منظور دقیقاً هفت بار عمل کردن نیست، بلکه منظور این است که پس از عمل «بسیار»، نتیجه بگیر. در زبان روسی نیز ضرب المثلی است به این مفهوم که «هفت نفر منتظر یک نفر نمیمانند» که باز هم منظور این است که تعداد زیادی منتظر یک نفر نمیمانند. همچنین در داستانها ،وقتی از پادشاهی صحبت میشود که در قصریست که هفت برج و بارو دارد، و یا هفت دریا، هفت سرزمین، هفت آسمان و ... همه جا «هفت»،به معنای بسیار به کار رفتهاست. عدد سیزده نیز چنین سرنوشتی دارد. دوازده را «دوجین» میگفتند و چون پس از آن را نمیشناختند، روی آن نام «دوجین شیطانی» گذاشتند. از اینجا، عدد سیزده نحس شد، چرا که پس از دوازده برای آنها ناشناخته بود و خبر از ابهام و تاریکی میداد. البته پیش آمدها یا روایتهایی هم به نحسی سیزده کمک کرد؛ مانند روایتی که در شام آخر، نفر سیزدهم به عیسای مسیح خیانت کرد و او را لو داد، وگرنه عدد ۱۳ با عددهای دیگر هیچ تفاوتی ندارد. (نمونههای دیگری هم از اینگونه، برای برخی عددها داریم. چهل چراغ به معنای درست ۴۰ چراغ نیست. هزار پا به معنای این نیست که این جانور ۱۰۰۰ پا دارد.) برخی عددها هم نشانه عدد شماری بودهاست. دست پنج انگشت دارد و اغلب چیزها را به یاری انگشتان دست و پا میشمردند. واژه پنج از پنجه گرفته شده است؛ زیرا پنجه دارای ۵ انگشت است. در زبان فارسی، واژه سی با واژه سه، هم ریشهاست. همینطور چهل با چهار، پنجاه با پنج و ... ولی واژه بیست، هیچ ربطی به واژه «دو» ندارد. این نشانه آن است که عدد ۲۰ به معنای مجموعه انگشتان دست و پاست و در زمانهای دور، مبنای عدد شماری بودهاست. در زبان فرانسوی به بیست میگویند «وَن» که هیچ ربطی به (دو=deux) ندارد. به جز آن، به هشتاد میگویند «چهار بیست تاً و به نود میگویند»چهار بیست تا و ده تاً. تنها در دورهای از پیشرفت تمدن به بی پایان بودن عددهای طبیعی پی بردند و به عنوان نمونه، اقلیدس (سده سوم پیش از میلاد) ثابت کرد، تعداد عددهای اول، بی نهایت است. اعداد حسابی همان اعداد طبیعی هستند که صفر هم به آنها اضافه شده است. به عبارت دیگر به مجموعهی اعداد زیر ، اعداد صحیح یا اعداد درست گویند و آن را با Z نمایش میدهند: { ... , 3 , 2 , 1 , 0 , 1- , 2- , 3- , ...} = Z درواقع اعداد صحیح شامل اعداد طبیعی مثبت و اعداد طبیعی منفی و عدد صفر است. این اعداد همانند اعداد طبیعی جزء مجموعه های شمارش پذیر نامتناهی است. شاخه ای از ریاضیات که به مطالعه در مورد ویژگیهای اعداد صحیح می پردازدنظریه اعداد نام دارد. صحیح همانند اعداد طبیعی نسبت به اعمال جمع و ضرب بسته است،یعنی جمع و ضرب هر دو عدد صحیح، یک عدد صحیح است. و چون اعداد صحیح شامل اعداد منفی و صفر می باشند بنابراین بر خلاف اعداد طبیعی نسبت به عمل تفریق نیز بسته اند.ولی چون حاصل تقسیم دو عدد صحیح بر هم ممکن است عددی صحیح نباشد،پس نمیتواند نسبت به عمل تقسیم بسته باشد. اعداد طبیعی اعداد طبیعی، اعدادی هستند که برای شمردن به کار میروند. مجموعه اعداد طبیعی {... ,۳ ,۲ ,۱} است.
در این مجموعه عدد صفر وجود ندارد و با اضافه کردن آن، مجموعه اعداد حسابی به وجود میآید. این مجموعه یک مجموعه نامتناهی است. در ریاضیات، مجموعه اعداد طبیعی را با نماد N نمایش میدهند. این حرف از آغاز واژه انگلیسی Natural، به معنای طبیعی، گرفته شده است. اعداد گنگ اعداد اصم اعداد گنگ، یا اعداد اصم، اعدادی حقیقی هستند که گویا نباشند، یعنی نتوان آنها را به صورت کسری که صورت و مخرجش عدد صحیح باشند نوشت. مجموعه اعداد گنگ مجموعهای ناشمارا است ولی میتوان اعداد گنگ را روی محور اعداد نمایش داد كار بسیار ساده ایی است كافی است هندسه را در ریاضیات مورد استفاده قرار دهیم . امتحان كنید میتوان از رابطه فیثاغورث استفاده كرد .
بری دیدن بقیه بر روی ادامه مطلب کلیک کنید
اعداد اول اعداد اول اعدادی طبیعی هستند که بر هیچ عددی بجز خودشان و عدد ۱ بخشپذیر نباشند. تنها استثنا عدد ۱ است که جزو این اعداد قرار نمیگیرد. اگرعددی طبیعی وبزرگتر از ۱ اول نباشد مرکب است. عدد یکان اعداد اول بزرگتر از ۱۰ فقط ممکن است اعداد ۱، ۳، ۷، ۹ باشد. اعداد اول جزو یکی از معماهای ریاضی باقیمانده است و هنوز کسی به فرمولی برای آنها به دست نیاورده است. سری اعداد اول به این صورت شروع میشود: ۲، ۳، ۵، ۷، ۱۱، ۱۳، ۱۷، ۱۹ ... قضیه ۱: تعداد اعداد اول بینهایت است. برهان: حکم را به روشی که منسوب به اقلیدس است اثبات میکنیم: فرض کنید تعداد اعداد اول متناهی و تعداد آنها n تا باشد. حال عدد M را که برابر حاصلضرب این اعداد به علاوه ۱ را در نظر بگیرید. این عدد مقسومعلیهی غیر از آن n عدد دارد که با فرض در تناقض است. قضیه ۲ (قضیه اساسی حساب): هر عدد طبیعی بزرگتر از ۱ را به شکل حاصلضرب اعدادی اول نوشت. قضیه ۳ (قضیه چپیشف):اگر n عددی طبیعی و بزرگتر از ۳ باشد، حتما" بین n و ۲n عدد اولی وجود دارد. قضیه ۴ هر عدد زوج را میتوان بصورت جمع سه عدد اول نوشت. قضیه ۵ هر عدد فرد (شامل اعداد اول) را میتوان به صورت جمع سه عدد اول نوشت (اثبات بر پایه قضیه ۴) قضیه 6-هر عدد فرد را میتوان به صورت دو برابر یك عدد اول بعلاوه یك عدد اول دیگر نوشت. خواص اعداد اول: 1- هر عدد اول برابر است با 6n+1 یا 6n-1 كه n یك عدد صحیح است. 2-مجذور هر عدد اول برابر است با 24n+1. 3-تفاضل مجذورهای دو عدد اول مضربی از 24 است. 4-حاصلضرب هر دو عدد اول بجز 2و3 مضربی از 6 بعلاوه یا منهای یك است. توان چهارم هر عدد اول بجز 2و3 مضربی از 240 بعلاوه یك است. بزرگترین عدد اول کشف شده برابر دو به توان ۳۰میلیون و ۴۰۲هزار و ۴۵۷منهای یك است.این عدد یک عدد مرسن است. عدد مرسن عددی است که برابر 2 به توان n منهای یک است. لازم به ذكر است كه تعداد 3000 عدد اول در سایت مگاسندر www.megasender.orgl وجود دارد و افرادی كه مایل به دریافت بیشتر این اعداد هستند می توانند با سایت مذكور تماس گرفته و تعداد بیشتری از آنها را بر روی لوح فشرده دریافت نمایند و طراحان این سایت خودشان این اعداد را محاسبه نموده اند عدد جبری اعداد جبری در ریاضیات اعدادی هستند که جواب معادلهای به شکل زیر باشند: anxn + an−1xn−1 + ··· + a1x + a0 = 0 ضریبهای a0 تا an در این معادله چند جملهای اعداد گویا هستند. تمام اعداد گویا اعداد جبری هم هستند. بعضی از اعداد حقیقی عدد جبری نیستند. عددی که جبری نباشد عدد متعالی (یا غیرجبری) نامیده میشود. اعداد حقیقی میدان تمام اعداد گویا و گنگ را اعداد حقیقی گویند و آن را با R نمایش میدهند. اعداد حقیقی را میتوان با اضافه کردن عدد موهومی( 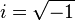 ) بسط داد. اعدادی به فرم a + bi که در آن a و b هر دو عدد حقیقی هستند را اعداد مختلط مینامند. ) بسط داد. اعدادی به فرم a + bi که در آن a و b هر دو عدد حقیقی هستند را اعداد مختلط مینامند. اعداد صحیح اعداد صحیح به مجموعهٔ اعداد طبیعی مثبت، اعداد طبیعی منفی، و عدد صفر گفته میشود. در ریاضیّات، معمولاً این مجموعه را با Z یا (ابتدای کلمه آلمانی Zahlen به معنی اعداد) نشان میدهند. همانند مجموعهٔ اعداد طبیعی، مجموعهٔ اعداد صحیح نیز یک مجموعهٔ شمارای نامتناهیست. شاخهای از ریاضیّات که به مطالعهٔ اعداد صحیح میپردازد، نظریهٔ اعداد نام دارد. خواص جبری همانند اعداد طبیعی، Z نیز نسبت به دو عمل جمع و ضرب بسته است. این بدان معناست که حاصل جمع و حاصل ضرب دو عدد صحیح، خود، یک عدد صحیح است. بر خلاف مجموعهٔ اعداد طبیعی، از آنجا که اعداد صحیح منفی، و به ویژه، عدد صفر هم به Z تعلق دارند، این مجموعه، نسبت به عمل تفریق نیز بسته است. اما Z تحت عمل تقسیم بسته نیست، زیرا خارج قسمت تقسیم دو عدد صحیح، لزوما عددی صحیح نخواهد بود. برخی از خواصّ اساسی مربوط به عملیّات جمع و ضرب در جدول زیر گنجانیده شده است (در اینجا b ،a، و c اعداد صحیح دلخواه هستند. جمع ضرب بسته بودن: a + b یک عدد صحیح است a × b یک عدد صحیح است شرکت پذیری: a + (b + c) = (a + b) + c a × (b × c) = (a × b) × c تعویض پذیری: a + b = b + a a × b = b × a وجود یک عنصر واحد: a + 0 = a a × 1 = a وجود یک عنصر عکس: a + (−a) = 0 توزیع پذیری: a × (b + c) = (a × b) + (a × c) نداشتن مقسوم علیههای صفر: اگر ab = 0، آنگاه a = 0 یا b = 0 مطابق بالا، خواصّ بسته بودن، شرکت پذیری و جابه جایی (یا تعویض پذیری) نسبت به هر دو عمل ضرب و جمع، وجود عضو همانی (واحد، یا یکّه) نسبت به جمع و ضرب، وجود عضو معکوس فقط نسبت به عمل جمع، و خاصیّت توزیع پذیری ضرب نسبت به جمع از اهمیت برخوردارند. در مبحث جبر مجرد، پنج خاصیّت اوّل در مورد جمع، نشان میدهد که مجموعهٔ Z به همراه عمل جمع یک گروه آبلی است. امّا، از آن جا که نسبتZ به ضرب عضو وارون (یا معکوس) ندارد، مجموعهٔ اعداد صحیح، به همراه عمل ضرب، گروه نمیسازد. مجموعهٔ ویژگیهای ذکر شده حاکی از این است که ، به همراه عملیّات ضرب و جمع، یک حلقه است، امّا، به دلیل نداشتن وارون ضربی، میدان نیست. مجموعهٔ اعداد گویا را باید کوچکترین میدانی دانست که اعداد صحیح را در بر میگیرد. اگرچه تقسیم معمولی در اعداد صحیح تعریف شده نیست، خاصیّت مهمّی در مورد تقسیم وجود دارد که به الگوریتم تقسیم مشهور است. یعنی به ازاء هر دو عدد صحیح و دلخواه a و b) b مخالف صفر)، q و r منحصر به فردی متعلق به مجموعه اعداد صحیح وجود دارد، به طوریکه: a = q.b + r که در این جا، q خارج قسمت و r باقیمانده تقسیم a بر b است. این کار اساس الگوریتم اقلیدس برای محاسبه بزرگترین مقسوم علیه مشترک را تشکیل میدهد. همچنین در جبر مجرد، بر اساس خواصی که در بالا ذکر شد، یک دامنه اقلیدسی است و در نتیجه دامنه ایدهآل اصلی میباشد و هر عدد طبیعی بزرگتر از یک را میتوان به طور یکتا به حاصلضرب اعداد اوّل تجزیه کرد (قضیه اساسی علم حساب.) اعداد گویا اعداد گویا1 حاصل تقسیم دو عدد صحیح بر یکدیگرست، به شرطی که عدد دوّم (مقسوم علیه) صفر نباشد. به بیان دیگر، هر عدد گویا را میتوان به شکل a/b یا آ بیم نوشت (که a و b اعداد صحیحاند). در ریاضیات، مجموعه اعداد گویا را، عموماً، با Q نمایش میدهند. به عنوان مجموعهای شمارا (یا قابل شمارش)، ولی نامتناهی، مجموعهٔ اعداد گویا، خود، زیرمجموعهایست چگال (dense) از مجموعهٔ بزرگتر و عمومیتر اعداد حقیقی. به عنوان یک اشتباه نسبتاً رائج، گاهی اعداد کسری را با اعداد گویا یکی میدانند. این در حالیست که، اعداد گویا فقط کسرهایی هستند که از تقسیم دو عدد صحیح حاصلآمده باشد. به عنوان نمونه، نسبت رادیكال سه دوم کسر هست، ولی، گویا نیست. اعداد مختلط عدد مختلط عددی به فرم a + bi است که در آن a و b از اعداد حقیقی و i عدد موهومی برابر با ریشهٔ دوم عدد ۱- است. اعداد مختلط از کجا آمدند همان طور که میدانید یک معادله درجه دو مثل ax2 + bX + c = 0 در اعداد حقیقی وقتی که Delta = b2 − 4avc مقداری منفی باشد گوئیم جواب ندارد.این یعنی اداد حقیقی شمول همه اعداد نیست پس اعداد مختط تعریف شدد. عدد مختلط a + bi را میتوان به صورت (a,b) نوشت. برای اینکه مفهوم اعداد مختلط را نتوجه شوید ،ابتدا باید با اعداد مختلط آشنایی کامل داشته باشید. عداد مختلط: می خواهیم معادله را حل کنیم.این معادله درمجموعه های دارای جواب نیست. برای اینکه هیچ عددی بتوان 2 و به علاوه 1 صفر نمیشود.همچنین اگرعددی به توان زوج برسد،غیرممکن است که علامت آن منفی شود.«با به پشت مساوی بردن معلوم معادله(1+) می بینیم که مجهول عددیست که به توان رسیده ومنفی شده که محال است».اما باید گفت که اعداد را با علامت دیگری غیر از+و- شان میدهیم؛ آن علامت شامل اعداد مختلط و متناهی می شود. در اعداد متناهی این قانون هست که عددی با بتوان زوج رسیدن منفی هم بشود.این اعداد رابا علامت نشان می دهند. برای یک عدد حقیقی( )عدد متناهی را به صورت زیر نشان میدهند: اعدادی راکه دارای علامت i هستند را موهومی می گوئیم. پس باتوجه به مطالب فوق دریافته ایدکه:جواب معادله درمجموعه ی اعداد متناهی دارای دو جواب است: i,+i- اعداد متناهی: به نظر شما اگر دلتای معادله ی درجه دومی منفی بودچطور می توان ریشه معادله موردنظر را پیداکرد؟ می خواهیم معادله ی را حل کنیم. حل: ازطرفی: ملاحظه می کنیم دو جوابی که بدست آمده اند بطورخالص نه حقیقی و نه موهومی به شمار می روند. لذاچنین اعدادی را در گروه اعداد مختلط جای دارند. یک عدد مختلط به صورت زوج مرتب :z=(x,y)معرفی می شوند.x: مولفه حقیقی و y: مولفه موهومی نام دارد. اعداد مختلط را می توان بصورت روبرو نشان داد: z=x+iy مزدوج آنر بصورت روبرو نشان می دهیم: 85.133.173.228 ۱۷:۲۸, ۱۹ ژوئیه ۲۰۰۶ (UTC) هرگاه مولفه های دو عدد مختلط دو به دو برابر بود؛آنرا؛دو عدد مختلط برابرنامیده می شود. نکته:این اعداد همچون سایر مجموعه اعداد دارای خواصص توزیع پذیری،شرکت پذیری و جابجایی نیز هست. میدان اعداد مختلط () میدان اعداد حقیقی () را به صورت زیر میدان، شامل میشود. درضمن z=(x,y) --->: x:مولفه حقیقی است و y:مولفه موهومی است. عدد مركب عدد مرکب عددی طبیعی بجز یک است که اول نباشد. عدد e عدد ای (e) یکی از ثابتهای ریاضی و پایه لگاریتم طبیعی است. عدد e تا ۲۹ رقم پس از ممیز چنین است: e = 2.71828 18284 59045 23536 02874 7135 ثابت شده است که e عددی گنگ و نیز عددی متعالی است. عدد پی ثابت ریاضی π (پی)، عددی حقیقی، تقریباً برابر با 3.14159 است که نسبت محیط دایره به قطر آن را در هندسهی اقلیدسی مشخص میکند و کاربردهای فراوانی دارد در ریاضیات، فیزیک و مهندسی دارد. عدد پی همچنین به ثابت ارشمیدس نیز معروف است.
فرمول های ریاضییک ضلع × خودش = مساحت مربع یک ضلع × 4 = محیط مربع طول × عرض = مساحت مستطیل 2× (طول + عرض) = محیط مستطیل 2 ÷ (قاعده × ارتفاع) = مساحت مثلث مجموع سه ضلع = محیط مثلث نصف ارتفاع × (قاعده بزرگ + قاعده کوچک) = مساحت ذوزنقه مجموع 4 ضلع = محیط ذوزنقه 2÷ (قطر بزرگ × قطر کوچک) = مساحت لوزی یک ضلع × 4 = محیط لوزی ارتفاع × قاعده = مساحت متوازی الاضلاع مجموع دو ضلع متوالی × 2 = محیط متوازی الاضلاع عدد پی × مجذور شعاع = مساحت دایره 14/3 × شعاع × شعاع 14/3 × قطر = محیط دایره مساحت کره چهار ×عدد پی × مجذور شعاع = مساحت کره حجم کره عدد پی × شعاع به توان 3 = حجم کره 14/3 × (نصف قطر کوچک × نصف قطر بزرگ) = مساحت بیضی
یک ضلع × تعداد اضلاع = محیط چند ضلعی منتظم طول یال × مساحت یک وجه = حجم مکعب ارتفاع × عرض × طول = حجم مکعب مستطیل ارتفاع × قاعده = حجم مکعب ارتفاع هرم × مساحت قاعده هرم = حجم هرم ارتفاع × مساحت قاعده = حجم استوانه ارتفاع × محیط قاعده = مساحت جانبی سطح دو قاعده + مساحت جانبی = سطح کل استوانه مجموع مساحت سطوح جانبی = مساحت جانبی منشور مجموع مساحت دو قاعده + مجموع مساحت سطوح جانبی = مساحت کلی منشور ارتفاع × مساحت قاعده = حجم مخروط تعاریف هندسی شعاع : خطی از مرکز دایره به پیرامون دایره را شعاع می گویند. (شعاع خطی مستقیم است که مرکز دایره را به نقطه ای از محیط دایره وصل می کند) شعاع نصف قطر است. قطر : فاصله مستقیم دو طرف دایره را که از وسط دایره بگذرد را قطر می نامند. عدد پی : 14/3 = π یکی از معروف ترین ثابت های ریاضی عدد π می باشد. عدد پی نسبت محیط دایره به قطرش است و تقریبا برابر 14/3 می باشد. و دقیقتر آن 14159/3 و دقیقتر آن تا 22 رقم اعشاری برابر است با : 1415926535897932384626/3 = π عدد پی (π) عددی گنگ است که رقم هایش تا بی نهایت ادامه دارد. *برای بدست آوردن مساحت و محیط دایره، کره و بیضی از عدد ثابت پی استفاده می شود. زاویه حاده (زاویه تند) : زاویه کوچکتر از 900 را حاده یا تند گویند. زاویه قائمه : برابر 900 می باشد. زاویه منفرجه (زاویه باز) : زاویه بیشتر از 900 را زاویه باز یا منفرجه نامند. زاویه نیم صفحه : زاویه 1800 را زاویه نیم صفحه گویند. همانند نیم دایره درجه = واحد اندازه گیری زاویه، درجه است. حداکثر زاویه (تمام صفحه) 360 درجه است. همانند دایره نیم ساز : نیم خطی که زاویه را به دو قسمت مساوی تقسیم می کند را نیمساز زاویه گویند. دو خط عمود بر هم : دو خط که زاویه بین آنها راست یا 900 باشد دو خط عمود بر هم هستند. عمود منصف : عمود منصف خطی است که هم عمود بر پاره خط بوده و هم آن را نصف کرده باشد. خط تقارن = اگر شکلی را از وسط تا کنیم طوری که تمامی زوایای آن شکل بر هم منطبق شوند، محل تا شدگی را خط تقارن نامند. بخش پذیری اعداد حاصل تقسیم صفر بر هر عددی برابر صفر است. حاصل تقسیم هر عددی بر صفر تعریف نشده است. یا می توان گفت بی نهایت است. اعدادی بر 2 قابل تقسیم هستند که یکان آنها زوج باشد. اعدادی بر 3 قابل تقسیم هستند که مجموعشان بر 3 قابل تقسیم باشد. اعدادی بر 4 قابل تقسیم هستند که دو رقم آخر آنها بر 4 قابل تقسیم باشد. هر عددی که مضربی از 100 باشد نیز بر 4 قابل تقسیم است. (چون 100 خودش بر 4 قابل تقسیم است.) اعدادی بر 5 قابل تقسیم هستند که رقم یکان آنها 0 یا 5 باشد. اعدادی بر 6 قابل تقسیم هستند که بر 2 و 3 قابل تقسیم باشند. عددی بر 8 قابل تقسیم است که یا مضربی از 1000 باشد و یا 3 رقم آخر آن بر 8 قابل تقسیم باشد. اعدادی بر 9 قابل تقسیم هستند که مجموعشان بر 9 قابل تقسیم باشد. عددی بر 10 قابل تقسیم است که رقم آخر آن صفر باشد. عددی بر 11 قابل تقسیم است که اگر ارقام آن عدد را به ترتیب از چپ به راست یکی در میان منها و جمع کنیم، حاصل صفر یا مضربی از 11 باشد. اعدادی بر 12 قابل تقسیم هستند که بر 3 و 4 قابل تقسیم باشند. اعدادی بر 14 قابل تقسیم هستند که بر 7 و 2 قابل تقسیم باشند. اعدادی بر 15 قابل تقسیم هستند که بر 3 و 5 قابل تقسیم باشند. هر تقسیم از چهار قسمت تشکیل شده است : مقسوم، مقسوم علیه، خارج قسمت، باقیمانده. باقیمانده + مقسوم علیه × خارج قسمت = مقسوم
اعداد اعداد طبیعی : اعداد صحیح بزرگتر از صفر را اعداد طبیعی گویند. N = {1, 2, 3, 4, 5,…..} اعداد صحیح : مجموعه اعداد مثبت و منفی صحیح را اعداد صحیح نامند. Z = {…,-3,-2,-1, 0, 1, 2, 3,…} اعداد اعشاری : 5/71 و 14/3 اعداد اول اعداد اول : هر عدد طبیعی بزرگتر از 1 که غیر از خودش و 1 مقسوم علیه دیگری نداشته باشد، عدد اول نامیده می شود. P = {2,3,5,7,11,13,17,19,23,29,31,37,41,43,……} اعداد مثبت : کلیه اعداد بزرگتر از صفر اعداد مثبت هستند. 5 و 1 اعداد منفی : کلیه اعداد کوچکتر از صفر اعداد منفی هستند. -6 , -3 اعداد کسری : ، ، ، هر عدد به صورت که در آن a , b اعداد صحیح می باشند و b ≠0 باشد یک کسر نامیده می شود. اعداد گویا : هر عددی که بتوان به صورت کسر نوشت یک عدد گویا است. اعداد گویا را با Q نمایش می دهند. هر عدد صحیح یک عدد گویاست. عدد گنگ : عددی که قابل تبدیل به نسبت دو عدد درست نباشد، عدد گنگ (اصم) است. اعداد گنگ را با (Q`) نمایش می دهند. مجموعه اعداد گویا و گنگ را اعداد حقیقی گویند و با (R) نمایش می دهند. متر متر = صد سانتیمتر یک متر است. کیلومتر = 1000 متر یک کیلومتر است. سانتی متر = 10 میلیمتر یک سانتی متر است. میلیمتر = یک میلیمتر برابر 1000 میکرون است. دسی متر = 10 سانتیمتر یک دسی متر است. دکامتر = 10 متر هکتو متر = 100 متر ذرع = 104 سانتیمتر متر مربع برابر است با مربعی که هر ضلع آن 1 متر باشد. 1 اینچ = 54/2 سانتیمتر 1 فوت = 5/30 سانتی متر 1 یارد = 44/91 سانتی متر 1 مایل = 609/1 کیلومتر هکتار = 10.000 متر مربع جریب = 4050 متر مربع 1 کیلومتر مربع = 100 هکتار لیتر واحد اندازه گیری مایعات لیتر است. لیتر = یک لیتر برابر است با گنجایش مکعبی تو خالی که هر بعد آن 10 سانتیمتر باشد. یک لیتر آب تقریبا برابر یک کیلوگرم می باشد. سانتی متر مکعب = حجم مکعبی که هر یک از ابعاد آن 1 سانتی متر باشد، یک سانتی متر مکعب است. متر مکعب = یک متر مکعب گنجایش مکعبی تو خالی به ابعاد یک متر است. 1000 لیتر برابر یک متر مکعب است. سی سی = یک سانتیمتر مکعب برابر یک سی سی است . یک لیتر = برابر 1000 سی سی است. اوزان و مقیاس ها گرم = هزار گرم برابر است با 1 کیلوگرم کیلوگرم = 1000 گرم تن = 1000 کیلوگرم من = 3 کیلوگرم خروار = 100 من سیر = 75 گرم چارک = 750 گرم قیراط = 9/205 گرم 1 اونس = 35/28 گرم 1 پوند = 592/453 گرم 1 ری = 12 کیلو گرم 1 مثقال = 6875/4 گرم 1 نخود : 1953/0 گرم 1 گندم = 0488/0 گرم واحدهای شمارش : انسانها از گذشته تا کنون برای شمارش اشیاء از اصطلاحات زیر استفاده می کنند : انسان (شتر و درخت خرما) = نفر کشتی و هواپیما = فروند پرندگان = عدد خانه ، مغازه = باب کتاب = جلد کاغذ = برگ دسته های کاغذ و مقوا = بند پارچه و کالاهای تجاری = عدل
استوانه: (Cylinder) نام شکلی است که دو قاعده دارد که دو دایره مساوی هستند و بر جانبی راست استوار است.
اگر مستطیل را حول طول آن دوران دهیم, شکل فضایی حاصل استوانه نامیده می شود. در این صورت طول مستطیل ارتفاع استوانه و عرض آن شعاع قاعده استوانه می باشد.
در شکل بالا مستطیل ABCD را حول طول آن دوران داده ایم و استوانه بوجود آمده است. رابطه های مهم: ارتفاع×مساحت قاعده(دایره) = حجم استوانه ارتفاع×محیط قاعده(دایره) = مساحت جانبی استوانه مساحت دو قاعده + مساحت جانبی = مساحت کل استوانه
منشور: (Prism) منشور در لغت به معنی پراکنده, نشر شده, زنده شده و مبعوث است و در اصطلاح هندسه نام شکلی است که دو قاعده دارد که دو چند ضلعی مساوی هستند و بدنه منشور(سطح جانبی منشور ) از مستطیلها یا متوازی الاضلاع ها تشکیل شده است.
í نام شکل: منشور 5 پهلو í یال های منشور: 'EE',DD',CC',BB',AA í وجه منشور: هر کدام از مستطیل های جانبی را یک وجه منشور می نامند. í ارتفاع منشور: از آنجا که هر کدام از یال ها بر دو قاعده منشور عمود می باشند, لذا ارتفاع منشور با اندازه هر یک از یال ها برابر است. í قاعده ی منشور: منشور دو قاعده دارد. ABCDE و 'A'B'C'D'E که دو پنج ضلعی مساوی اند. رابطه های مهم: ارتفاع × مساحت قاعده = حجم منشور ارتفاع × محیط قاعده = مساحت جانبی منشور مساحت دو قاعده + مساحت جانبی = مساحت کل منشور
هرم: (pyramid) هرم در لغت به معنی سخت پیر گردیدن و کلان سال شدن است و در اصطلاح هندسه حجمی است که قاعده آن یک چند ضلعی و وجوه جانبی اش مثلثهایی باشند که همه به یک رأس مشترک(رأس هرم) منتهی می شوند.
í نام شکل: هرم منتظم. í رأس هرم: نقطه S í ارتفاع هرم: پاره خطی است که از رأس هرم به مرکز قاعده ی هرم عمود است(SO) í قاعده هرم: پنج ضلعی منتظم ABCDE í سهم هرم: ارتفاع مثلث های جانبی, ارتفاع هر وجه جانبی هرم منتظم(SH). í وجه هرم: هر یک از مثلث هایی که بدنه هرم را می پوشانند را یک وجه جانبی می نامیم. í یال هرم: محل تقاطع هر دو وجه جانبی را یال هرم می نامیم. SE,SD,SC,SB,SA
رابطه های مهم: مخروط : (cone) مخروط به معنی خراشیده شده ، تراشیده شده و خراطی شده است ودر اصطلاح هندسه حجمی است که از دوران مثلث قائم الزاویه حول یک ضلع آن به دست می آید . کله قند و کلاه بوقی نمونه هایی به شکل مخروط هستند.
معرفی مخروط : í نام شکل : مخروط í رأس :نقطه ی s í ارتفاع :پاره خط SO ضلعی که مثلث قائم الزاویه را حول آن دوران داده ایم تا مخروط بوجود آید. پاره خطی است که از رأس مخروط بر صفحه ی قاعده ی آن عمود است . í قاعده ی مخروط : دایره c به مرکز O و شعاع oB را قاعده ی مخروط می نامیم. í مولد مخروط :پاره خط SA یا SB ، وتر مثلث قائم الزاویه که مخروط را بوجود آورده است. رابطه های مهم :
کره : (sphere) کره به معنی گوی و آن چه که به شکل گوی باشد، است و در اصطلاح هندسه شکلی است که از دوران نیم دایره حول قطرش بوجود می آید . مانند توپ ، گوی چوگان
معرفی کره: í مرکز کره :نقطه ی O í شعاع کره :R (فاصله ی نقاط روی سطح کره از مرکز کره) í دایره ی عظیمه :اگر یک کره را نصف کنیم، دایره ای که از نصف کردن کره بدست می آید، دایره عظیمه نام دارد .
رابطه های مهم :
 این کتاب با تمام دقت و جزییات دانش اموزان را با مباحث انالیز حقیقی اشنا می سازد. مباحث کتاب عبارتند از فضاهای متریک، مجموعه باز و بسته، دنباله همگرا، محدودیت عملکرد و تداوم، مجموعه فشرده، توالی و مجموعه ای از توابع، سری، مشتق گیری و انتگرال، قضیه تیلور، ، و شرایط کافی از انتگرالپذیری. و بیش از 500 تمرین. نام کتاب:Mathematical Analysis I نویسندگان :by Elias Zakon انتشار :The Trillia Group 2004 تعداد صفحات : 367 فرمت فایل:PDF حجم فایل : 2.5MG زبان کتاب : انگلیسی برای دانلود اینجا کلیک کنید. |
----------------- -------------------------- |















