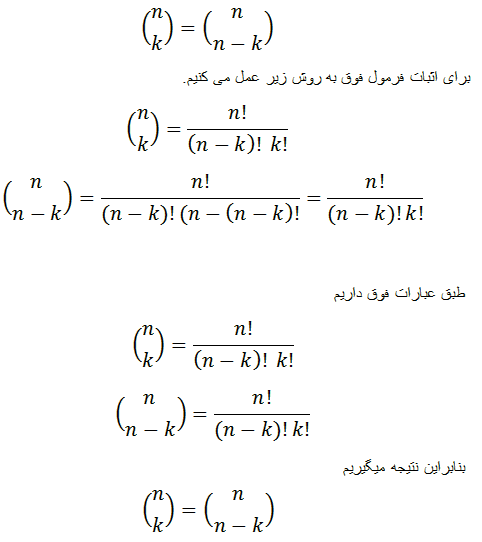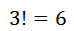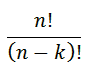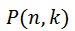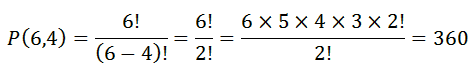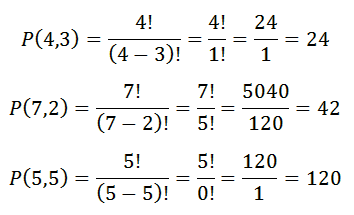|
مقاله دانشجویی تحقیق پروزه ومفالات دانشجویی
|
||
|
|
حل معادلات درجه سوم و چهارم کتاب تشریح مسائل حساب دیفرانسیل و انتگرال آدامز  اعداد حقیقی اعداد مختلط اعداد مختلط و تبدیلات صفحه دنباله عددی و سری عددی تابع های پیوسته مفهوم حد مفهوم مشتق تقریب خطی نمودار تابع و کاربرد های آن بهینه سازی چند جمله ای تیلور انتگرال یک متغییری قضیه اساسی حساب دبرانسیل و انتگرال انتگرال توابع گویا محاسبه تقریبی انتگرال انتگرال های ناسره سری تیلور و سری توانی سری فوریه و… برای دانلود اینجا کلیک کنید ....
مباحث این کتاب مفید :
مفاهیم پایه معادلات دیفرانسیل و انتگرال ، معادلات دیفرانسیل مرتبه اول، معادلات مرتبه دوم دیفرانسیل، تبدیل لاپلاس، سیستم های معادلات دیفرانسیل، راه حل های سری، نظم بالاتر معادلات دیفرانسیل و مسائل مقدار مرزی و سری فوریه، معادلات دیفرانسیل با مشتقات جزئی و...
نام کتاب:Differential Equations نویسندگان : Paul Dawkins انتشار : Lamar University 2011 تعداد صفحات : 504 فرمت فایل:PDF حجم فایل : 3MG زبان کتاب : انگلیسی
 این کتاب بدون وارد شدن به جزییات به نظریه اساسی احتمال،معادلات دیفرانسیل تصادفی و تعدادی از کاربردهای این مباحث می پردازد، فرض بر این است که خواننده این کتاب با مباحث نطریه احتمال، معادلات دیفرانسیل معمولی و معادلات دیفرانسیل با مشتقات جزیی اشنایی نسبی دارد . نام کتاب:An Introduction to Stochastic Differential Equations نویسندگان :Lawrence C. Evans انتشار :UC Berkeley 2006 تعداد صفحات : 139 فرمت فایل:PDF حجم فایل : 1MG زبان کتاب : انگلیسی Download link
 نام کتاب:Notes on Differential Equations نویسندگان :Bob Terrell انتشار :2005 تعداد صفحات : 99 فرمت فایل:PDF حجم فایل : 1MG زبان کتاب : انگلیسی Download link
 نام کتاب:Elementary Differential Equations
نویسندگان : Boyce, DiPrima فرمت فایل:PDF حجم فایل : 13MB زبان کتاب : انگلیسی
 معادلات دیفرانسیل با مشتقات جزیی در معنای اصلی ارایه ی مدل های ریاضی در علوم ،مهندسی،و زمینه های دیگر است.نویسنده در این کتاب به بحث های پایه این درس پرداخته است از جمله معادلات سهموی،بیضوی،هذلوی،و...
این کتاب یک انتخاب عالی برای دانش اموزان و معلمان در بخش علوم ریاضیات و هم چنین علوم مهندسی و کامپیوتر می باشد. نام کتاب:Numerical solution of partial differential equations نویسندگان : Morton & Mayers فرمت فایل:PDF حجم فایل : 4MG زبان کتاب : انگلیسی
سرفصلها: فصل 1: چند جمله ایهای متعامد فصل 2 :تابع گرین و مسائل اشترم _ لیوویل فصل 3:سری فوریه و انتگرال فوریه فصل 4 :معادلات دیفرانسیل با مشتقات جزئی مرتبه دوم فصل5 : معادلات دیفرانسیل با مشتقات جزئی مرتبه دوم فصل6: کاربرد های فیزیکی معادلات دیفرانسیل با مشتقات جزئی برای دانلود اینجا کلیک کنید
کتاب Boyce & Diprima یکی از معروف ترین کتاب های معادلات دیفرانسیل می باشد، این جزوه اموزشی پاورپینت توسط جمال صفار اردبیلی تهیه شده است که علاوه بر قضایای مهم مثال های حل شده ی خوبی را دارا می باشد. پیشنهاد:ابتدا این جزوه اموزشی را به طور کامل فرا بگیرید سپس تمارین کتاب بویس را حل کنید تا به راحتی از پس سوالات امتحانات پایان ترم و حتی ازمون کارشناسی ارشد بر آیید. البته خود کتاب معادلات دیفرانسیل بویس را نیز می توانید از قسمت معالات دیفرانسیل در ارشیو موضوعی دانلود کنید. مباحث این جزوه اموزشی: فصل اول: معادله دیفرانسیل مرتبه اول فصل دوم: معادله دیفرانسیل مرتبه دوم فصل سوم: حل معادله دیفرانسیل به روش سری ها فصل چهارم:توابع بسل وخواص آن فصل پنجم:دستگاه معادلات دیفرانسیل
این کتاب شامل مجموعه ای از بهترین ایده ها در انالیز مختلط است ، برخی از قسمت های کتاب عبارتند از: اعداد مختلط؛ پایه تجزیه و تحلیل پیچیده، تمایز پیچیده، انتگرال های پیچیده، قضیه انتگرال کوشی، فرمول انتگرال کوشی، سری تیلور، اصل حداکثر، نقاط تکین و لوران سری، قضیه انتگرال کوشی مجدد، نظریه باقی مانده، ارزیابی انتگرال معین توابع همساز و تعیین conformal موبیوس تحولات شوارتز کریستوفل تحولات، همگرایی یکنواخت و... Chapter 2: FOUNDATIONS OF COMPLEX ANALYSIS Chapter 3: COMPLEX DIFFERENTIATION Chapter 5: CAUCHY'S INTEGRAL THEOREM Chapter 6: CAUCHY'S INTEGRAL FORMULA Chapter 7: TAYLOR SERIES, UNIQUENESS AND THE MAXIMUM PRINCIPLE Chapter 8: ISOLATED SINGULARITIES AND LAURENT SERIES Chapter 9: CAUCHY'S INTEGRAL THEOREM REVISITED Chapter 11: EVALUATION OF DEFINITE INTEGRALS Chapter 12: HARMONIC FUNCTIONS AND CONFORMAL MAPPINGS Chapter 13: MÖBIUS TRANSFORMATIONS Chapter 14: SCHWARZ-CHRISTOFFEL TRANSFORMATIONS Chapter 15: LAPLACE'S EQUATION REVISITED Chapter 16: UNIFORM CONVERGENCE
 نام کتاب:Lectures in Basic Computational Numerical Analysis نویسندگان :by James M. McDonough انتشار : University of Kentucky 2001 تعداد صفحات : 166 فرمت فایل:PDF حجم فایل : 2MG زبان کتاب : انگلیسی Download link
 فصل 1: مقدمه و مفاهیم اساسی فصل 2: روش های عددی برای معادلات خطی و ماتریس ها فصل 3: چندجملهای تقریب، درونیابی و چندجمله ای متعامد فصل 4: بررسی عددی مشتق و انتگرال فصل 5: حل عددی معادلات دیفرانسیل و انتگرال فصل 6: حداقل مربعات، تجزیه و تحلیل فوریه، و هنجارهای تقریب مرتبط فصل 7: تئوری احتمال و آمار فصل 8: نمونه توزیع لحظات، آزمایش های آماری، و روش نام کتاب:Fundamental Numerical Methods and Data Analysis نویسندگان :George W. Collins, II انتشار :NASA ADS 2003 تعداد صفحات :254 فرمت فایل:PDF زبان کتاب : انگلیسی برای دانلود هر قسمت از کتاب بر روی ان کلیک کنید.
جزوه اموزشی انالیز عددی 1 که مولف اصلی کتاب ان دکتر اسماعیل بابلیان است توسط محسن ساعدی در اسلاید های پاور پوینت تهیه شده است،این جزوه منبع خوبی برای یادگیری اولیه انالیز عددی می باشد. سرفصل های این جزوه: فصل اول : خطاها فصل دوم: حل معادلات غیر خطی فصل سوم: حل معادلات چند جمله ای فصل چهارم : درونیابی فصل پنجم: مشتق گیری وانتگرالگیری فصل ششم: حل عددی معادلات دیفرانسیل... برای دانلود اینجا کلیک کنید.
سرفصل های این کتاب 187 صفحه ای : قصل اول : مروری بر حساب دیفرانسیل و انتگرال فصل دوم:منابع خطا فصل سوم:حل معادلات غیر خطی فصل چهارم:درونیابی فصل پنجم : تقریب برای دانلود اینجا کلیک کنید.
 مباحث : فصل اول : حل سیستمهای خطی فصل دوم : مقادیر و بردارهای ویژه فصل سوم : حل عددی معادلات دیفرانسیل
 مباحث : فصل اول : خطاها فصل دوم : حل معدلات غیر خطی( f( x مساوی با صفر فصل سوم : درون یابی و برون یابی فصل چهارم : مشتق گیری و انتگرال گیری عددی .... پسورد فایل فشرده شده : mathbook.mihanblog.com برای دانلود اینجا کلیک کنید. حجم : 13 مگابایت
صرفه جویی در وقت و هزینه
1- سرشماری جمعیت،کار عظیم ووقت گیر و پرهزینه ایه مخصوصا برای کشورهایی با ده ها میلیون جمعیت،انجام دادن سرشماری در هر سال کار غیر معقولیه به همین خاطر این کار رو هر ده سال یک بار انجام میدن. اطلاعات حاصل از سرشماری بسیار ارزشمنده و برای برنامه ریزیهای کلان یک کشور یا بررسی روندی که اون کشور در مورد مسائل مختلف در حال طی کردنشه یا پیش بینی اتفاقات آینده،مورد استفاده قرار میگیره.حالا اگر بتونیم بجای اینکه این اطلاعات رو ده سال به ده سال داشته باشیم،سال به سال یا حتی ماه به ماه داشته باشیم این مسئله میتونه در روند رو به رشد جامعه بسیار بسیار مفید باشه،اما همونطور که گفته شد انجام سرشماری با بازه های زمانی کمتر از ده سال به دردسرهاش نمی ارزه.آیا راهی نیست که سرشماری رو ده سال یکبار انجام بدیم اما از همون اطلاعات برای بدست آوردن اطلاعات سالیانه یا حتی ماهیانه استفاده کنیم؟2- اجازه بدید کمی دقیق تر به این مسئله نگاه کنیم.فرض کنید یک نمودار داریم که محور x اون سالها رو نشون میده و محور y اون جمعیت یک کشور رو در هر سال.سرشماری انجام شده در هر ده سال یک نقطه رو در اون نمودار مشخص میکنه.فرض کنید طی 50 سال 5 سرشماری انجام شده پس ما 5 نقطه روی این نمودار داریم اما اگه بتونیم به نوعی این نقاط رو به هم وصل کنیم میتونیم تابع جمعیت در سال رو پیدا کنیم و با کمک اون تابع،جمعیت رو در هر سال یا ماهی (خارج از زمان سرشماری)مشخص کنیم.به این اتصال نقاط به هم برای ساختن تابع،درونیابی (Interpolation) میگن. 3- درونیابی در جاهای مختلفی مورد استفاده قرار میگیره مثلا فرض کنید شرکتی میخواد در یک مناقصه ی سود آور جهت ساخت یک بزرگراه شرکت کنه.مسیر طولانی و هزینه ها در حد چندین میلیارد تومانه.این شرکت از کجا میتونه بفهمه که برای ساخت این بزرگراه چه مقدار خاکبرداری و خاکریزی لازمه تا هزینه ها رو مشخص کنه و هزینه ی پیشنهادیش رو در مناقصه ارائه کنه؟ تنها راه استفاده از درونیابیه. متخصصین نقشه برداری اون شرکت،طول و عرض و ارتفاع چندین نقطه از مسیر رو محاسبه میکنن و به کمک این اطلاعات و درونیابی،به یک نقشه ی سه بعدی ازمسیر دست پیدا میکنن که دیگه با اون براحتی میشه هزینه ها رو برآورد کرد و در مناقصه برنده شد!!! 4- سر و کله ی درونیابی در بسیاری از آزمایشهای هزینه بر یا زمان بر هم پیدا میشه. مثلا فرض کنید مجبور باشید مقداری طلا رو در محلولی حل کنید و دمای واکنش حاصل از حل طلا در محلول رو اندازه بگیرید.در این حالت هر چه تعداد آزمایشهاتون کمتر باشه هزینتون کمتره پس اینجا هر چه درونیاب دقیق تری داشته باشید میتونین هزینه کار رو پایین تر ببرید.یا ممکنه برنامه ای کامپیوتری نوشتید که پارامتر خاصی رو به عنوان ورودی می گیره و عدد خاصی رو به عنوان خروجی به شما میده و اجرای این برنامه هم ساعتها طول میکشه.خب طبیعیه که شما نمیتونین پارامتر ورودیتون رو به میزان کمی افزایش بدین و برنامتون رو اجرا کنید چون این کار میتونه هفته ها وقتتون رو بگیره پس پارامترتون رو زیاد افزایش میدین و بعدا از دورنیابی استفاده می کنید. 5- در گذشته هم درونیابی اهمیت زیادی داشت چرا که مثل الان،ماشین حسابهای پیشرفته و کامپیوتر و نرم افزارهای قدرتمند ریاضی در دسترس نبود.در اون روزها برای بدست آوردن جدول سینوس یا لگاریتم که کار زمان بر و دشواری بود تنها مقادیر خاصی(مثلا اعداد حسابی 0 و 1 و 2 و ..) رو در نظر میگرفتن و اطلاعات رو بصورت جدولی ارائه میکردن.حالا اگه یه نفر سینوس یا لگاریتم مقداری اعشاری رو میخواست باید از درونیابها استفاده می کرد. درونیابی چه فرقی با تقریب داره؟!!!
منبع : daneshju6- حالا که این همه راجع به اهمیت درونیابی صحبت کردیم، فرض کنید چند نقطه که باید برای درونیابی مورد استفاده قرار بگیرند رو پیدا کردین و حالا هدفتون وصل کردن اون نقاط به هم و بدست آوردن یک تابع درونیابیه که تا حد ممکن رفتاری شبیه تابع اصلی داشته باشه . ساده ترین راه برای اتصال نقاط به هم اینه که اونها رو با یک خط مستقیم به هم وصل کنیم (درونیابی خطی) اما آیا مثلا در مثال سرشماری، رشد جمعیت خطی بوده؟ نه الزاما !!! ممکنه در سال خاصی یک بلای طبیعی یا بیماری همه گیر یا مهاجرت رخ داده باشه و جمعیت در اون سال بطور غیر خطی افزایش یا کاهش پیدا کرده باشه پس اتصال نقاط بطور خطی میتونه خطای زیادی داشته باشه پس بهتره راههای دیگه ای رو امتحان کنیم. 7- اگه تابع رو طوری بسازیم که بصورت یک چند جمله ای باشه، چند مزیت بزرگ خواهیم داشت.چند جمله ایها، توابع شناخته شده ای هستند و کار باهاشون راحته و براحتی میتونیم مشتق و انتگرالشون رو بگیریم. راههای زیادی برای بدست آوردن چند جمله ای درونیاب وجود داره مثل روش لاگرانژ،روش نیوتون،روش نویل و روش هرمیت. همینطور میتونیم درونیابی رو با توابعی بجز چند جمله ایها انجام بدیم مثلا درونیابی گویا که در اون تابع بصورت کسری که در صورت و مخرجش چند جمله ای قرار داره، محاسبه میشه یا چند جمله ای نمایی یا مثلثاتی که بترتیب از توابع نمایی و مثلثاتی(سینوس و کسینوس) برای درونیابی استفاده می کنند. 8- درونیابی به روشهای اخیر دو مشکل بزرگ داره.اول اینکه ممکنه نوسانات تابع درونیاب (علی الخصوص برای درونیاب چند جمله ای با درجه بالا) خیلی زیاد بشه و خطای درونیابی به شدت بالا بره.دوم هم اینکه اگه ما یک نقطه به نقاط اولیه اضافه کنیم (مثلا اطلاعات یک سال دیگه رو به اطلاعات سرشماری اضافه کنیم) تابع درونیاب بدست اومده کلا عوض میشه!!! برای رفع این مشکل از درونیابی با اسپلاینها استفاده میشه.اسپلاینها بر خلاف درونیابهای گفته شده که اطلاعات رو بطور سراسری (global) درونیابی می کردن،اطلاعات رو بطور موضعی (local) درونیابی می کنند. اسپلاینهای مکعبی(Cubic Spline) و بی-اسپلاین ها(B-Spline) امروزه کاربردهای بسیاری در مقاصد عملی مثل مدل سازی های پزشکی،صنایع اتومبیل سازی، گرافیک کامپیوتر و پردازش تصاویر دارند. 9- در بعضی موارد نقاط بدست آمده طی آزمایش که برای پیدا کردن تابع درونیاب مورد استفاده قرار می گیرند بگونه ای هستند که اگر از درونیابی استفاده کنیم(یعنی تابع را دقیقا از نقاطی که طی آزمایش بدست آمده عبور دهیم) تابع فرمی پیچیده پیدا میکند مثلا در بعضی نقاط مشتق پذیر نیست (تابع در اون نقطه به شکل نوک تیز است) یا نوسانات زیادی دارد. اینجاست که بجای درونیابی از تقریب(Approximation) استفاده میکنیم یعنی بجای اینکه تابع را دقیقا از نقاط عبور دهیم و به تابعی پیچیده برسیم، تابع را از بین نقاط برازش می کنیم یعنی تابع را بگونه ای میسازیم که بجای اینکه دقیقا از نقاط عبور کند از نزدیک نقاط عبور کند اما در عوض تابع حاصله فرمی ساده داشته باشد تا کار با آن آسان باشد. 10- جالب آنکه گاهی ما خود تابع را داریم اما در کارهایمان به علت پیچیدگی آن تابع، از تقریبش بجای خود آن تابع استفاده می کنیم.مشهورترین روش تقریب، تقریب کمترین مربعات است. در این روش تابع تقریب، بگونه ای انتخاب می شود که فاصله ی آن تا نقاط، می نیمم شود.این روش وزن یکسانی را در طول بازه ی تقریب اعمال می کند که ممکن است منجر به خطای زیاد در تقریب شود.در این حالت از تقریب کمترین مربعات وزن دار استفاده می شود تا خطای تقریب کاهش یابد.
 این کتاب با استفاده از یک رویکرد روشن و بسیار دقیق خوانندگان را به درک درستی از مفاهیم ریاضی و تجزیه و تحلیل ان می رساند . این کتاب برای کسانی که می خواهند به درک درستی از تجزیه و تحلیل های ریاضی دست یابند نوشته شده است.در این کتاب سعی بر این است که با به چالش کشیدن دانشجو او را در درک بالایی از مفاهیم برساند.
نام کتاب:Introduction to Real Analysis نویسندگان :William F. Trench انتشار :Prentice Hall 2003 تعداد صفحات : 583 فرمت فایل:PDF حجم فایل : 3.5MG زبان کتاب : انگلیسی سلام دوستان
 سلام دوستان
در این پست کتاب انالیز حقیقی ALIPRANTIS به همراه حل المسائل ان را برای شما قرار داده ایم.... برای دانلود حل المسائل کتاب اینجا کلیک کنید.
 سلام دوستان،در این پست طبق در خواست یکی از دوستان (دنیز)انالیز حقیقی و مختلط والتر رودین را به همراه حل المسائل کامل ان برای شما عزیزان قرار داده ایم،این کتاب ویژه سال اول کارشناسی ارشد می باشد که در ان روش ها و قضایای اصلی انالیز به نحوی ارائه شده اند که بر روابط بین شاخه های مختلف ان قویا تاکید دارند.
مباحث این کتاب ارزشمند به شرح زیر است: 1 انتگرال گیری مجرد 2اندازه های بورل مثبت 3فضای L^p 4نظریه مقدماتی فضای هیلبرت 5چند نمونه از روشهای فضای باناخ 6اندازه های مختلط 7مشتقگیری 8انتگرال گیری بر فضاهای حاصل ضربی 9تبدیلات فوریه 10خواص مقدماتی توابع هلوریخت 11تابع های توافقی 12اصل مدول ماکسیمم 13تقریب به وسیله توابع گویا 14نگاشت همدیس 15صفرهای توابع هلوریخت 16تداوم تحلیلی 17فضاهای H^p 18نظریه مقدماتی جبرهای باناخ 19تبدیلات فوریه هلوریخت 20تقریب یکنواخت به وسیله چند جمله ای ها..... دانلود کتاب با فرمت DJVU دانلود حل المسائل
برای دانلود هر کدام از فصل های کتاب فقط کافی است بر روی فصل مورد نظر کلیک کنید.
SECTION A --- BASIC MATERIAL
Chapter 2: RELATIONS AND FUNCTIONS
Chapter 3: THE NATURAL NUMBERS
Chapter 4: DIVISION AND FACTORIZATION
SECTION B --- COMPUTATIONAL ASPECTS
Chapter 6: FINITE STATE MACHINES
Chapter 7: FINITE STATE AUTOMATA
Chapter 9: GROUPS AND MODULO ARITHMETIC
Chapter 10: INTRODUCTION TO CODING THEORY
Chapter 12: PUBLIC KEY CRYPTOGRAPHY
SECTION C --- MATHEMATICAL ASPECTS
Chapter 13: PRINCIPLE OF INCLUSION-EXCLUSION
Chapter 14: GENERATING FUNCTIONS
Chapter 15: NUMBER OF SOLUTIONS OF A LINEAR EQUATION
Chapter 16: RECURRENCE RELATIONS
شاید در ریاضیات گسسته با مسأله ی زیر برخورد كرده باشید:
 شاید در ریاضیات گسسته با مسأله ی زیر برخورد كرده باشید:
 طرح این مسأله، انگیزهای برای معرّفی مفاهیم زیر میباشد. E.C.Catalan
در واقع این روش یك تناظر یك به یك بین كلماتی به طول اكنون به مسألهای كه در آغاز مقاله مطرح كردیم، برمیگردیم.
ب) یك 2+n ضلعی محدّب در نظر بگیرید. با وصل كردن رأسها، میتوان این چند ضلعی را به مثلثهایی افراز كرد.
 نام کتاب:Combinatorial Algorithms نویسندگان : Albert Nijenhuis, Herbert S. Wilf انتشار :Academic Press Inc 1978 تعداد صفحات : 316 فرمت فایل:PDF حجم فایل : 5.5MG زبان کتاب : انگلیسی Download now
برای دانلود هر فصل کتاب بروی pdf file کلیک کنید.Table of Contents Preface Matroid Bundles, by Laura Anderson, 1-21 Combinatorial Representation Theory, by Hélène Barcelo and Arun Ram, 23-90 An Algorithmic Theory of Lattice Points in Polyhedra, by Alexander Barvinok and James E. Pommersheim, 91-147 Some Algebraic Properties of the Schechtman--Varchenko Bilinear Forms, by Graham Denham and Phil Hanlon, 149-176 Combinatorial Differential Topology and Geometry, by Robin Forman, 177-206 Macdonald Polynomials and Geometry, by Mark Haiman, 207-254 Enumeration of Matchings: Problems and Progress, by James Propp, 255-291 The Generalized Baues Problem, by Victor Reiner, 293-336 Littlewood--Richardson Semigroups, by Andrei Zelevinsky, 337-345 در این پست دانلود کتاب ریاضیت گسسته گریمالدی به همراه جزوه فارسی این کتاب را برای دانلود شما عزایزان قرار داده ایم.
1. جبر خطی و معادلات دیفرانسیل دانشگاه هاروارد 3. نظریه جبری اعداد نوشته رابرت بی اش 4. کتاب فوق العاده نظریه جبری اعداد و آخرین قضیه فرما نوشته یان استیوارت و داوید تال 5. کتاب جبر خطی پیشرفته نوشته استیون رومن 6. کتاب گروه های جایگشتی نوشته دیکسون 7. کتاب هندسه جبری نوشته شافارویچ 8. کتاب هندسه جبری نوشته هارت شورن 9. حل تمرین هندسه جبری هارت شورن 10. کتاب گروه های متناهی نوشته هاروی رز 11. کتاب گروه های متناهی نوشته آیزاک 12. کتاب جبر مدرن پیشرفته نوشته ژزف روتمن 13. کتاب هندسه جبری نوشته دنیل پرین 14. کتاب ایده ال ها ،واریته ها و الگوریتم ها (بهترین کتاب مقدماتی برای شروع هندسه جبری) 15. کتاب نظریه نمایش گروه ها نوشته مارتین آیزاک 16. حل تمرین نظریه نمایش گروه ها نوشته مارتین آیزاک 17. کتاب نظریه گروه ها نوشته زازنهاوس 18. کتاب رویای گالوا(نظریه گروه ها و حل پذیری معادلات دیفرانسیل) 19. کتاب دوره ای بر نظریه گروه ها 20. کتاب هندسه جبری نوشته دنیل پرین 21. کتاب چندین متغیر پیچیده و جبر نوشته باناخ 22. کتاب جبر و نظریه های بیضوی 25. یک مجموعه غیر قابل اندازه گیری 26. کتاب ترکیبیات جبری و پایه های گروبنر 28. کتاب الگوریتم ماتریس نوشته استوارت 29. کتاب برخی از جنبه های نظریه حلقه 30. کتاب جبر 1 تالیف دکتر نقی پور(دانشگاه شهر کرد) 31. کتاب جبر 2 تالیف دکتر نقی پور(دانشگاه شهر کرد)
34. هندسه اقلیدسی و نااقلیدسی - گرینبرگ 36- هندسه دیفرانسیل 1- اسپیواک 38- هندسه مقدماتی از دیدگاه پیشرفته 39 هندسه منیفلد 1- دکتر بیدآباد 40- هندسه منیفلد 2 - دکتر بیدآباد 43 آشنایی با هندسه دیفرانسیل - گوئتس 44 حسابان روی خمینه ها - اسپیواک 45 روش سریع تر اختنبرگ در حساب 47 - کتاب منیفلد های توپولوژیک - لی 48 - کتاب اساس هندسه و تئوری کاربردی 49 -کتاب طرحی از هندسه - داوید آیزنباد- هریس 50 - کتاب هندسه ی فراکتال ها، ابعاد پیچیده و توابع زتا 51 - کتاب نظریه اندازه گیری هندسی - مورگان 53- نظریه جبری اعداد - رابرت بی اش 54- کتاب نظریه جبری اعداد و آخرین قضیه فرما - یان استیوارت و داوید تال 55- کتاب هندسه جبری - شافارویچ 56- کتاب هندسه جبری - هارت شورن 57 حل تمرین هندسه جبری - هارت شورن 58 کتاب هندسه جبری - دنیل پرین 59 کتاب هندسه جبری - دنیل پرین 61- یک مجموعه غیر قابل اندازه گیری 62 - کتاب مسایل ریاضی و اثبات آنها (ترکیبیات، نظریه اعداد و هندسه) 63 -کتاب بی نظیر نظریه اعداد - ژان پیر سر 64 - کتاب 104 مشکل نظریه اعداد از IMO 65 - کتاب ریاضی گسسته در رشته علوم کامپیوتر 67 - کتاب ریاضیات گسسته و کاربرد آن - روزن 68 - کتاب روش های ترکیبی در ریاضیات گسسته 69 - کتاب نمای کلی از ریاضیات گسسته 70 - کتاب ترکیبات - پیتر کمرون 72 - جزوه ساختمان گسته (ریاضی گسسته) با حل تمرین و نمونه سوال
اگر تعدادی شیء متمایز داشته باشیم به هر نحوه ی قرار گرفتن آن ها در کنار هم یک جایگشت می گوییم.
بنابراین شش عدد سه رقمی بدون تکرار رقم می توان نوشت.
در ضمن این تعداد را با نماد زیر نیز نشان می دهند.
این نکته نیز قابل توجه است که همیشه n بزرگ تر یا مساوی k می باشد .
بنابراین 360 کلمه چهار حرفی می توان نوشت.
هدف اصلی این کتاب ارایه مقدمه ای منسجم و کارامد برای نظریه گراف است .این کتاب مناسب برای دانش اموزان پیشرفته در مقطع کارشناسی و ابتدای کارشناسی ارشد در رشته های ریاضی و علوم کامپیوتر است. برای دانلود هر قسمت از کتاب نیز بر روی لینک های زیر کلیک کنید.
سلام دوستان عزیز امروز یک جزوه مفصل گراف به زبان فارسی برای شما دوستان عزیز اماده کرده ام.این جزوه قدم به قدم شما را در یادگیری گراف جلو می برد. در این جزوه مسایل زیادی دیده می شود که دارای پاسخ روان و تشریحی نیز هستند. مباحث:الفبای گراف،مسیر،دور،گراف هم بند،ناهمبند،درخت،ماتریس مجاورت و...
پسورد:mathbook.mihanblog.com Downloadاگه مطالبی شبیه این میخوای رو لینکهای روبرو کلیک کن!!! : نظریه گراف
 این کتاب علاوه بر دروس براکت، ضرب،جمع ،تقسیم،معادلات ساده؛نتایج خاص در ضرب و تقسیم ،توان ،بزرگترین مقسوم علیه مشتریک،کوچک ترین مضرب مشترک،کسرها ،معادلات درجه 2 و معادلات همزمان و... را نیز داراست نام کتاب:Algebra for Beginners
نویسندگان : James Loudon انتشار :Copp, Clark & Co 1876 تعداد صفحات : 172 فرمت فایل:PDF حجم فایل : 7.7MG زبان کتاب : انگلیسی در این پست یک جزوه برای درس جبر 1 قرار داده ایم که مولف ان دکتر جمس بت داوود می باشد،مباحث این جزوه خوب به شرح زیر است:
در این پست جزوه جبر 2 که مولف کتاب ان مارین اچ فنریک بوده توسط دكتر خدیجه احمدی آملی تهیه شده است. مباحث : فصل اول . گروهها و حلقه ها (50 اسلاید) فصل دوم . توسیع میدانها (112 اسلاید) فصل سوم . تناظر گالوا (163 اسلاید) فصل چهارم . کاربردها (81 اسلاید) مجموع اسلایدها:406 Download |
----------------- -------------------------- |